株価の予測

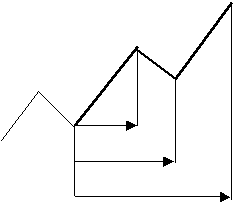
株価は時々刻々変化しています。このため「株価はいつもアンバランスな状態」にあると言えます。しかし、すわりの良い場所は一ヶ所だけあります。されは上がって来た株価が下げに転ずる屈折点です。

「株価はどれだけの時間で屈折点に達するのか？・・・そしてそこからいったいどこまでたどり着くのか？を研究してまいります。
○下降時の計算
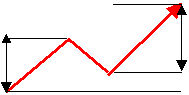
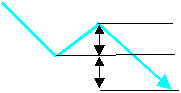
BからC時点までの上げ幅である20円の2倍となる40円をCの1,070円より減算した1,030円を株価のたどり着く先と予測する。
○下降時の計算
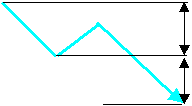
AからBまでの下げ幅50円をC時点の株価1,050円より減算した1000円をを株価のたどり着く先と予測する。

　

A(1,000)

A(1,000)

○上昇時の計算　
BからC時点までの下げ幅である20円の2倍となる40円をCの1,030円へ加算した1,070円を株価のたどり着く先と予測する。
◇屈折点

日であれば9,17,26,33,42,65,76,83日があげられる。
①9日
②17日or33日
③26日or42日

また、週でみれば9,13,17,21,26,33,42,65週があげられます。
①9週
②13週
③17週
●株価ごとにこの基本数値は違いますので、チャートからこのリズム を読み取りましょう！

　

A(1,000)

　

○下降時の計算
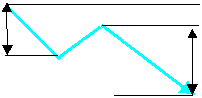
AからBまでの下げ幅50円をB時点の株価950円より減算した900円をを株価のたどり着く先と予測する。
◇「屈折点までの時間は？」
◇「株価予測　」・・・・・・ＣからDまでの株価を予測する方法。
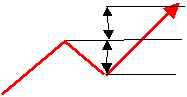
■V計算値　(　倍返し法　）

A

B

C

D

①

②

③

B(1,050)

C(1,030)

D(1,070)

20

20

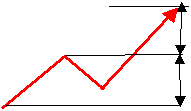
■E計算値　（　倍加法　）

B(1,050)

D(1,100)

50

50

○上昇時の計算
AからBまでの上げ幅50円をB時点の株価1,050円に加算した1,100円をを株価のたどり着く先と予測する。

C(1,030)
■N計算値法

B(1,050)

C(1,030)

D(1,080)

50

50

○上昇時の計算
AからBまでの上げ幅50円をC時点の株価1,030円に加算した1,080円をを株価のたどり着く先と予測する。
【上昇時　】
【下降時　】

A(2,000)

B(1,050)

C(1,070)

D(1,030)

20

20

【上昇時　】
【下降時　】

A(1,000)

B(950)

50

50

C(900)
【上昇時　】
【下降時　】

A(1,080)

B(1,030)

C(1,050)

D(1,000)

50

50